Left: Sensitivity map of a Chandra X-ray imaging observation. This is a 2-D image which provides an estimate of the probability that a source with a flux f_X in a certain energy band will be detected across the detector area. The sensitivity increases from the centre of the field of view (dark) to the edge (light grey) because of instrumental effects. Our Bayesian approach for estimating the sensitivity map correctly accounts for these effects as well as biases associated with the source detection. Right: The 1-D representation of the sensitivity map is the sensitivity curve, which provides an estimate of the total detector area in which a source with flux f_X can be detected. The continuous line is our new Bayesian approach, the dashed line is the standard way of estimating the sensitivity map and the sensitivity curve that does not account properly for the various sources of bias. The Bayesian sensitivity curve levels off at faint fluxes because such faint sources have a small but finite probability of producing fluctuations above the background level.

X-ray observations suffer complex instrumental effects that have a strong impact on the detection probability of point sources. The size and the shape of the Point Spread Function (PSF) for example, vary across the detector, while the sensitivity decreases from the centre to the edge of the field of view. Also, the application of any source detection software on an X-ray image introduces biases. Brighter sources have a higher probability of detection compared to fainter ones. Background fluctuations result in spurious detections that are inevitably present in any X-ray catalogue. Statistical variations of the source counts combined with the steep logN-logS of the X-ray source population result in brighter measured fluxes for the detected sources compared to their intrinsic ones (Eddington bias). For a wide range of applications it is important to quantify these effects accurately to understand the type of sources a given X-ray observation is (or is not) sensitive to.

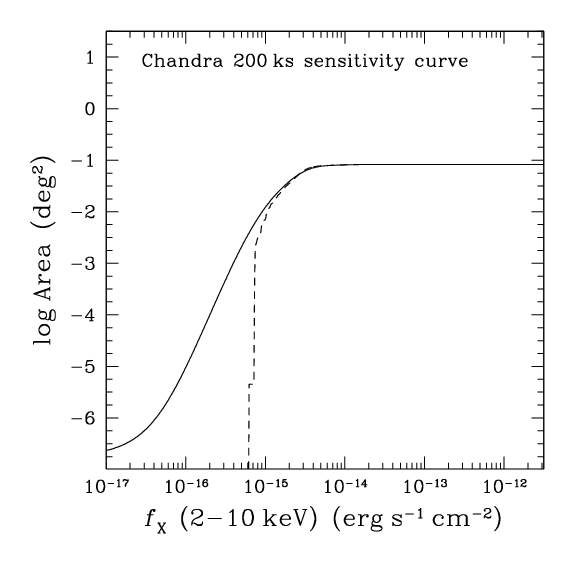
We have developed a Bayesian method for determining the sensitivity map of an X-ray imaging observation, which correctly accounts for the effects above and provides an accurate estimate of the probability that a source with a flux f_X in a certain energy band will be detected across the detector area (Georgakakis et al. 2008). This method is used to estimate the X-ray source counts. Because we correctly account for the completeness and flux bias corrections, particularly for sources with few photons close to the detection limit of a given survey, we have been able to extend previous determinations of the logN-logS to fluxes that are 1.5-2 times fainter.